Die Geschwindigkeit einer Faktorisierung ist jedoch nicht nur von der Größe der zu faktorisierenden Zahl ab, sondern auch von der Größe und Anzahl an Primfaktoren. So wird 23000 in weniger als einer Sekunde faktorisiert, obwohl 23000 eine 904-stellige Zahl ist. Besteht eine Zahl jedoch aus nur zwei großen Primzahlen, deren Differenz jedoch auch nicht zu klein sein darf, so dauert es deutlich länger, entsprechende Zahlen zu faktorisieren.
Die folgende Grafik zeigt die Zeiten, die MuPAD auf meinem Computer benötigt, um eine Zahl zu faktorisieren, die aus den beiden Primfaktoren
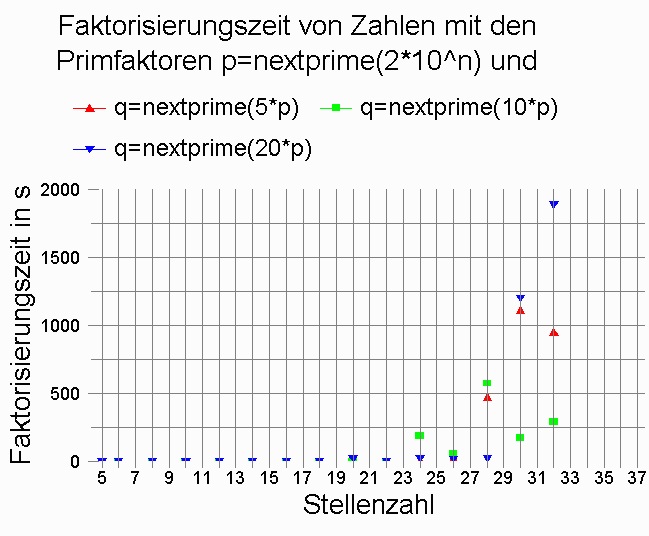 p:= nextprime(2*10n)
p:= nextprime(2*10n) und
q:=nextprime(c*p)
besteht, wobei für c=5, 10 und 20 eingesetzt wurden.
Falls noch Zeit ist, noch zwei Aufgaben zur Wiederholung der Kongruenzrechnung:
Aufgabe 5:
Bestimme jeweils die letzte Ziffer von 2461, 3531, 51231, 7331 und 113111 mit Hilfe der Kongruenzrechnung!
Aufgabe 6:
Zeige, daß 437-8713º 0 (mod 44)